1. INTRODUCCIÓN.

La Universidad Politécnica de Valencia tiene sus sedes en tres campus, el de Vera se sitúa en las afueras de la ciudad de Valencia por el límite norte, cerca de la salida de la ciudad por carretera y ferrocarril hacia Barcelona. El ambiente rural que rodea al campus y la distancia que la separa de la ciudad le confiere una identidad muy poco urbana.

No obstante, ésta situación no siempre fue así. La historia de la ciudad de Valencia en relación a la Universidad data de más de 500 años, cuando el núcleo poblacional era muy reducido y compacto, con una trama urbanística de herencia claramente medieval.

El edificio de la primera Universidad Valenciana, enclavado en el centro histórico y geográfico por excelencia de la ciudad, ancla el espíritu universitario a la identidad histórica de Valencia.

A lo largo de los siglos la presencia e influencia de estas instituciones educativas en la vida de los ciudadanos siempre había sido algo tangible, pero con el paso del tiempo, razones urbanísticas y demográficas de peso propiciaron un cambio.

Las universidades tuvieron que ampliar sus centros docentes y de servicios, y lo hicieron primero bajo una política de disgregación, adquiriendo inmuebles en los límites del casco urbano para construir sus ampliaciones, que pronto fueron absorbidos por el desarrollo imparable de la urbe; escuelas y facultades aparecieron dispersas e inconexas por toda la ciudad.

Finalmente, el precio al alza de los terrenos considerados limítrofes a la ciudad y la perenne necesidad de adecuación de las Universidades a la creciente demanda de plazas para estudiantes fueron el desencadenante de que los campus de las nuevas universidades y las ampliaciones de las más antiguas, se establecieran como núcleos urbanizados de nueva construcción en grandes extensiones de terreno situadas a una relativa distancia del casco urbano y en cierta forma aisladas; pensadas como comunidades que fuesen autosuficientes en la mayor medida posible e independientes de la ciudad.

Un regreso hipotético y nostálgico a la comunión entre Universidad y ciudad se propone en esta pieza y es posible gracias a la Realidad Aumentada. Varios edificios se introducen en el paisaje universitario en un juego visual y conceptual sumamente atrayente y lúdico que pretende unir en el mismo plano realidad e ilusión, periferia y centro, modernidad e historia.

Con este propósito, varios edificios históricos de la ciudad de Valencia seleccionados por ser considerados emblemáticos, monumentales y populares se han fotografiado con cámaras digitales, medido usando técnicas cartográficas y se han modelado buscando la máxima fidelidad posible técnica y visualmente al original en tres dimensiones, usando como textura final mapeada la real fotografiada.

El usuario lleva una computadora portátil en sus manos y percibe los objetos virtuales junto a los verdaderos vía un HMD (Head Mounted Display). El usuario puede moverse libremente por el interior de un área delimitada, y el mirar al paisaje descubre un nuevo entorno; en el espacio característico arquitectónico de la universidad, ya conocido, encuentra inmersos edificios virtuales propios del centro de esa misma ciudad, perfectamente integrados con los reales de la Universidad y respondiendo en cuanto a su orientación e iluminación a sus movimientos y encuadres, pudiendo experimentar la inmersión en un espacio interactivo de carácter monumental.

2. DESCRIPCIÓN GENERAL

2.1 Edificios históricos

Varios edificios históricos de la ciudad de Valencia se han seleccionado por ser considerados como emblemáticos, monumentales y populares. Las fotografías fueron tomadas con una cámara digital y desde múltiples puntos de vista con el fin de modelar los edificios, se usaron técnicas de fotogrametría para garantizar la  fidelidad con la realidad. Los modelos pueden ser construidos en diferentes formatos; en nuestro caso, hemos utilizado los .obj por ser compatible con OpenGL. Nuestro sistema permite la utilización de modelos complejos, por lo tanto, el gran número de polígonos que utilizan parece no afectar al render en tiempo real (ver sección 3.2). En la figura 1 y 1.1 se muestran las antiguas Torres de Serrano y el modelo 3D obtenido. Este monumento se utilizará como un ejemplo en las siguientes secciones.

Fig. 1 y 1.1

2.2 Escenario Realidad Aumentada

El usuario lleva un ordenador portátil en una mochila y se sumerge en el aplicación a través de un HMD. Montado sobre el HMD, hay una cámara y un sensor de movimiento inercial. La primera capta una imagen de vídeo de lo real y sirve como un sensor visual para lograr del usuario su posición y orientación dentro de la aplicación en tiempo real; el segundo se utiliza exclusivamente para detectar la orientación del usuario (ver sección 3.3). Él puede moverse libremente dentro de un área delimitada, el jardín redondeado de la facultad de Bellas Artes (figura 2), y mirando al paisaje descubre un nuevo entorno; en el conocido espacio arquitectónico de la Universidad, se encuentra inmerso con los edificios virtuales del centro de la ciudad, perfectamente integrados con los reales de la escuela, en un espacio virtual de carácter monumental.

3. METODOLOGÍA

La integración entre los edificios reales del campus y los virtuales del centro de la ciudad se lleva a cabo en varios pasos:

• En primer lugar, un sistema de coordenadas cartesianas 3D tiene que ser establecida en el campus, y los modelos de la ciudad, los edificios del centro, deben ser ‘colocados’ en él.

• En segundo lugar, el problema de la oclusión se debe tomar en cuenta.

• Por último, el punto de visión del usuario (es decir, la cámara centro de proyección) debe ser posicionado y orientado en tiempo real de acuerdo con el sistema de coordenadas del campus.

En las siguientes secciones, todos estos pasos se explican con más detalle.

3.1 3D–Campus, Marco de Referencia

Un sistema de coordenadas 3D se estableció para el campus siguiendo técnicas geodésicas. Este es un sistema cartesiano de coordenadas locales 3D, que se define con tres ejes ortogonales (X, Y, Z) y con su origen en (x0, y0, z0). Este sistema se denomina sistema de referencia de la escuela o simplemente marco campus. Un punto i, se ubicará en el sistema con sus coordenadas 3D (Xi, Yi, Zi). Las mediciones de los puntos de control disponibles en 3D se lograron con el fin de alinear los ejes Y a la dirección del Norte, por lo tanto el eje X está apuntando hacia el Este. El origen del eje Z coincide con el nivel medio del mar.
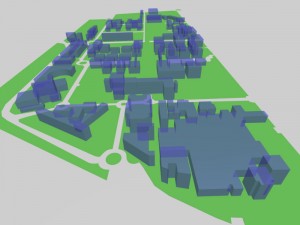
Se midieron todos los edificios del campus circundantes que toman parte en la aplicación Back to the 70’s para lograr un modelo 3D fiel en el marco del campus (figura 2). Estos puntos se midieron con un teodolito digital a través de la intersección de haz espacial. De hecho, sólo la altura de los edificios era de interés, ya que un mapa de todo el campus estaba disponible. Sin embargo, también se midieron algunos puntos a nivel de tierra con el fin de comprobar la fiabilidad del mapa. Se utilizó el modelo obtenido para tratar el problema de la oclusión, como se explicará en la siguiente sección.

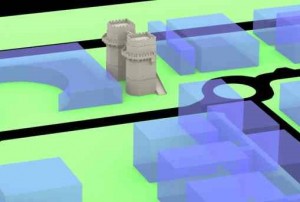Fig 2 y 2.1

3.2 Áreas de oclusión

Como se explicó en la sección anterior, un conjunto de objetos reales y virtuales se integran dentro del marco de referencia del campus. Para lograr una integración adecuada, las áreas de oclusión deberían tenerse en cuenta. Estas áreas son aquellas de los objetos virtuales ocultos por los reales, según el punto de vista del usuario. En la figura inferior (3) se muestra un ejemplo. Como se puede observar, el modelo de las Torres de Serrano se encuentra en el primer plano de la imagen, cuando debería estar parcialmente por detrás de la construcción real del edificio de Bellas Artes. En Back to the 70’s, este problema se resuelve con el programa MSP / Jitter Max, donde un modelo virtual del campus funciona como una máscara 3D con el fin de ocluir las partes de los modelos de ciudad escondidos en el campus. En la figura (3.1), las Torres de Serrano y los modelos virtuales de la escuela de Bellas Artes se ven juntos. La oclusión se gestiona mediante la adición como una textura a la máscara 3D (el modelo de campus) en tiempo real, sobre el vídeo capturado del entorno real. En la figura (3.2) se puede apreciar la combinación resultante.

Fig 3, 3.1, 3.2

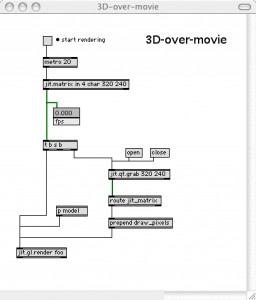
Jitter es básicamente un conjunto de vídeo, matriz y objetos gráficos en 3D para el entorno de programación gráfica Max Msp, que es especialmente util para el procesamiento de vídeo en tiempo real, efectos personalizados, gráficos 2D / 3D, audio / visuales interacctivos, visualización de datos, y análisis de los mismos. Dentro de este programa, se pueden crear objetos. Un conjunto de objetos que trabajan juntos se llaman un parche. En la figura 4 y 4.1 se muestra el parche principal utilizado en Back to the 70’s.

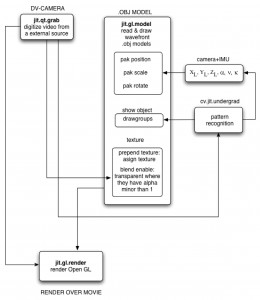Fig. 4, 4.1

La imagen procedente de la cámara a través del objeto jit.qt.grab se envía directamente a la jit.gl.render para aparecer como la imagen de fondo. Para lograr el efecto de oclusión, esto en tiempo real se procesa también la imagen de vídeo para reducir la imagen a blanco y negro, lograr un contraste máximo con jit.op, y cambiar de tamaño con srcret pak. Después de esto, la imagen de vídeo está lista para ser usada como la textura del modelo de campus 3D, que es, de hecho, la máscara de oclusión. Esta máscara se aplica al permitir actuar al componente de transparencia en el modelo de campus 3D, cuyos valores alfa deben ser inferior a 1, y así permanezca transparente. Por último, el modelo 3D de la imagen de vídeo, se toma con jit.gl.render OpenGL y se muestra en la ventana de salida llamada jit.window.

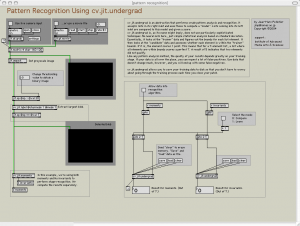Fig. 5, 5.1

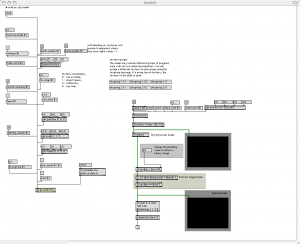
Otros parámetros importantes del procesamiento en tiempo real son la posición pak, la escala y la rotación pak pak. Estos están relacionados con la posición del usuario dentro de la aplicación. Según el punto de vista del usuario, los modelos 3D deben ser traducidos y / o girar a aparecer en la ventana de final en el lugar correcto (véase la sección siguiente). Este procedimiento se hace en nuestro sistema a través de la cv.jit parche que se basa en el cv.jit.undergrad objeto (figura 5 y 5.1), que realiza el análisis de patrones y reconocimiento.

3.3 Orientación Usuario

El usuario será orientado en Back to the 70’s, cuando la posición de la cámara y la inclinación relacionada con el marco de referencia del campus se conozcan. Esto se logra en dos pasos:

• En primer lugar, la orientación de la cámara absoluta en el marco de referencia campus se calcula con un tracking visual, que consiste en una cámara que detecta un campo 3D-de coordenadas.

• En segundo lugar, las orientaciones relativas que trabajan fotograma a fotograma se detectan directamente con una unidad de movimiento inercial (IMU), que detecta el movimiento del usuario dentro de la aplicación.

Ambos pasos se realizan en tiempo real y cada vez que se transmiten los puntos calibrados por la cámara, la orientación absoluta se calcula de nuevo. En las siguientes secciones, estos pasos se explican con más detalle.

3.3.1 Orientación absoluta de cámara

Esta técnica consiste en la localización del usuario – el centro de proyección de la cámara – dentro del marco de la escuela. Esto se soluciona con el cálculo de los parámetros de orientación de la cámara exterior que establecen la posición de proyección central y la inclinación de la imagen espacial de coordenadas en el marco campus. En Back to the 70’s, este paso se lleva a cabo con un tracking visual. La relación matemática entre los marcos del campus y de imagen se establece por las ecuaciones de colinealidad bien conocidos:

Para resolver el sistema en la ecuación, un mínimo de seis puntos homólogos – es decir, puntos identificables en los cuadros de imagen y de la escuela – se requiere, ya que cada punto genera dos ecuaciones. Estos puntos se denominan puntos de control, ya que sus coordenadas 3D del marco campus se conocen con una buena precisión. La disponibilidad de más de los puntos de control requeridas en el ajuste, se resuelve mediante un procedimiento de mínimos cuadrados, permite el cálculo de parámetros adicionales e incrementa la redundancia y la fiabilidad del sistema.
En Back to the 70’s, el proceso de DLT se consigue de forma automática en el programa Max / MSP Jitter. Cuando la cámara está viendo la calibración de pruebas de campo, el parche cv.jit (ver sección anterior) reconoce automáticamente los puntos de control y calcula su posición en el cuadro de imagen (xi, yi). Entonces se aplica la ecuación para lograr los parámetros de orientación de la cámara. Estos parámetros se envían entonces a la posición pak, la escala y la rotación pak pak. Los puntos de control tienen algunas propiedades especiales que hacen que el cv.jit los reconozca automáticamente. De hecho, son un conjunto de pequeños espejos fijos en fachadas de los edificios cuyas coordenadas 3D son conocidas y provistas de un pivote que les permite orientarse en la dirección del sol. Por lo tanto, estos puntos aparecen en la imagen muy luminosos y son fácilmente identificables a través del análisis de patrón y el reconocimiento realizado por cv.jit.
La principal ventaja de utilizar una DLT es que cualquier cámara se puede utilizar sin la necesidad de ser calibrada, y por lo tanto, este procedimiento se utiliza comúnmente en aplicaciones industriales, arquitectónicas, robótica y aplicaciones de visión por ordenador. Sin embargo, si no se cumplen algunas condiciones, pueden surgir problemas numéricos. Para evitar estos inconvenientes, los siguientes requisitos tienen que ser tomados en consideración:

• Los puntos de control no deben ser coplanares o pertenecer a un mismo plano.

• El origen del sistema de referencia no debe estar muy lejos de la calibración de la prueba de campo.

• Se debe evitar que, el plano paralelo al plano de imagen que contiene el centro de proyección, ya sea cerca o contiene el origen de la trama de referencia campus.

Estos requisitos condicionan directamente la ubicación de la prueba de calibración de campo, así como la posición de los puntos de control en su interior. En la figura 6 se muestra un esquema de una calibración de prueba de campo adecuado, dentro de que se cumplan todos los requisitos anteriores.

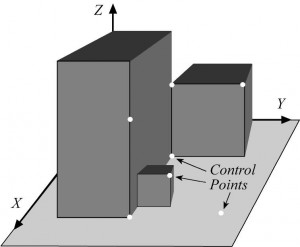Fig 6

3.3.2 relativa orientación de la cámara

Una vez que el usuario está orientado en el espacio, sólo traslaciones y rotaciones respecto a su posición absoluta obtenida inicialmente necesitan ser detectadas. Para medir estos parámetros, una IMU se puede utilizar, que es un dispositivo que mide de forma continua la aceleración 3D (giroscopio). Con estos valores medidos, el posicionamiento y la inclinación de un dispositivo en movimiento se pueden obtener en tiempo real. Los principios de la IMU se basan en la segunda ley de Newton, que describe el hecho de que la fuerza específica medida de un dispositivo de movimiento con respecto a un sistema inercial se puede obtener como una combinación lineal de las aceleraciones lineales del sistema y la aceleración gravitacional. La aceleración lineal se puede calcular a partir de la fuerza específica detectada. Las velocidades se obtienen mediante la integración una vez de las aceleraciones lineales, y el posicionamiento mediante la integración dos veces. Las mediciones de la tasa se ​​integran con respecto al tiempo a fin de lograr la inclinación de la información. La posición y la inclinación se pueden obtener en diferentes sistemas de coordenadas, como un marco de nivel local o una tierra fija geocéntrico de coordenadas cartesianas marco. El primero se utiliza muy a menudo para fines de navegación, ya que emite directamente las coordenadas geográficas y los ángulos de navegación.
Mediante el anclaje de la IMU a la cámara se logra la posición, velocidad y orientación de la propia cámara. Para asegurar la máxima precisión, la IMU debe ser relativamente pequeña y ligera para que pueda ser montada lo más cerca posible del centro de la proyección de la cámara. Una localización óptima del dispositivo IMU sería directamente en la parte superior de la cámara, de tal manera que ambos centros están alineados en los ejes verticales. Sin embargo, debido a que la cámara y los dispositivos IMU no ocupan físicamente el mismo lugar, un desplazamiento debe existir entre ellos y tienen que ser calibrados y considerado en el procedimiento de orientación relativa. La Figura 7 muestra un esquema de la relación espacial entre diferentes marcos.

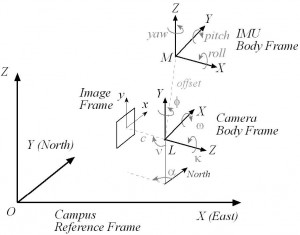Fig 7

Una desventaja de la IMU es que su precisión disminuye con el tiempo, y por lo tanto se requieren mediciones de actualización externa, es decir, existe la necesidad de que el sistema sea inicializado con frecuencia a través de la prueba de calibración de campo. Por esta razón, mientras que el usuario está dentro de Back to the 70’s, se debe realizar con regularidad la calibración de la prueba de campo. Sin embargo, como la calibración de prueba de campo se integra adecuadamente en el espacio, este procedimiento es una tarea natural.

4. CONCLUSIONES

Hemos presentado una aplicación de Realidad Aumentada, Back to the 70’s, que muestra un entorno virtual de una alternativa / presente hipotética, por lo que responde a las preguntas de cómo  podría ser hoy en día el campus de Vera si sus orígenes no se hubieran movido, y cómo sería su integración en el centro de la ciudad de Valencia.
Desde un punto de vista conceptual, podemos destacar que la utilización de elementos arquitectónicos populares del centro de la ciudad, que poseen una identidad histórica y emblemática de primer orden, y su incorporación en un entorno de una nueva construcción relativa, da pie a una confrontación visual, que propicia diversas interpretaciones conceptuales igualmente válidas y atractivas. Especialmente interesante es la combinación del pasado y el presente, a través de una curiosa metáfora: prácticamente anula las distancias físicas para mostrar conjuntamente diversos elementos que no pueden ser nunca vistos juntos en la esfera real, debido a sus dimensiones monumentales y el espacio distante que ocupan. También podemos pensar que nosotros hacemos lo mismo con el tiempo, mientras unimos elementos arquitectónicos de diferentes épocas. Entonces, la identidad del espacio experimentado por la mediación de esta aplicación de realidad aumentada es integrador y totalmente nuevo.

Las contribuciones tecnológicas en este documento son la integración de elementos virtuales en los reales, y preservar los últimos de una oclusión visual no deseada. El uso de un modelo 3D del campus con su textura siendo una imagen detectada en tiempo real, sirve como una máscara que se actualiza continuamente de acuerdo con el movimiento del usuario, mostrando siempre una oclusión adecuada según su punto de vista. Importante es también la combinación exitosa de dos sensores diferentes, una cámara y un dispositivo de IMU, para rastrear la orientación del usuario y los movimientos dentro de la aplicación. Dentro de esta técnica, una orientación inicial se consigue mediante un sistema de tracking visual: una cámara detecta un conjunto de pequeños espejos que sirven como puntos de control de una calibración de prueba de campo para lograr la posición de la cámara a través de un procedimiento de DLT. Orientaciones relativas y sucesivas se realizan a continuación con un dispositivo de IMU, que debe ser inicializado regularmente por el tracking visual para evitar derivas. Y por último, pero no menos importante, la capacidad del sistema para hacer que los modelos, construidos a través de métodos fotogramétricos, bastante complejos, por que constan de una gran cantidad de polígonos, se visualicen en tiempo real, mientras se ejecuten los algoritmos necesarios para conseguir la orientación del usuario y resolver el problema de la oclusión.

Participantes